事実は,その「アイヌ」は "アイヌ" (「アイヌ」を自称する者) であって,アイヌ (アイヌ文化を生きる者──これは終焉した) ではない。 さらに,"アイヌ" には,ホンモノもニセモノもない。 どういうことか? "アイヌ" の「アイヌ」自称は,「自分はアイヌの子孫」と言っていることになる。 「自分はアイヌの子孫」の意味は,「自分の先祖のうちに,アイヌが少なくとも一人いる」である。 ──先祖のなかにアイヌが何人いるかは,"アイヌ" の間で競うものにはならないからである。 ところで,「自分の先祖のうちに,アイヌが少なくとも一人いる」は,だれにも可能性のあることである。 どういうことか? 自分の先祖を溯行してみる。 自分の父母,その父母それぞれの父母,その父母それぞれの父母,‥‥。 n代溯ったときの先祖の総数は: \[ \ \ \ \ \sum_{i=1}^n 2 \ (2^{i - 1}) = \frac{2 \ (2^{n} - 1)}{2 - 1} = 2 \ (2^{n} - 1) \] これがどんな数かというと:
20代溯ったときは,2 (1048576 - 1) = 2157150 もちろん,実際にはこんな感じで先祖の数が増えるわけではない。 この計算には,<一人が重複して数えられている>が含まれている。 しかし重複カウントがあることを踏まえても,先祖の拡散がすさまじいものになりそうだということはわかる。 この「先祖拡散」に,アイヌの移動・「混血」を重ねて考えてみる。 例えば,「東北アイヌ」を考えてみる。(  東北アイヌ) 東北アイヌ)
これの子孫 (即ち,自分の先祖のうちに少なくとも一人東北アイヌがいる者) は,地勢上,全国に拡散していることになる。 そして,東北アイヌの始まりが古いほど,子孫の全国拡散は大きなものになる。 著しくは,東北アイヌが『続日本紀』に出てくる「 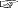 『続日本紀』) のようなのと一部重なるかも,という場合である。 『続日本紀』) のようなのと一部重なるかも,という場合である。
このタイムスケールだと,自分の先祖溯行の計算は,
40代溯ったときは,2 (1099511627776 - 1) = 2199023255550 - (重複カウント) こんな計算になるわけであるから,「自分の先祖のうちに,アイヌが少なくとも一人いる」はだれにも可能性のあることになる。 よって,「自分の先祖のうちに,アイヌが少なくとも一人いる」は,言ってもしようがないものになる。 だれが "アイヌ" を振る舞っても,ホンモノもニセモノもないわけである。 |