Up 錐の体積の求め方 更新: 2024-11-21

    いまさらだが，ちょっと気が向いて，「錐の体積の求め方」を書いて見ることにした。
    本サイトの「学校数学の主題」は 2000年より前に書いたものが主で，そのとき「錐」については「錐の体積」を書いていなかったのである。
    理由は，数式を書くのが面倒。
    実際，少し込み入った数式は，画像で作成して，ページに貼り付ける他なくて，これが面倒だった。
    しかしその後，数式の記述言語である Tex が使えるウェブライブラリが登場した。
    本サイトは MathJax を使っているが，これは「2009年にプロジェクト開始」というものである。
    で，いまは，その気になればそんなに面倒がらずに書ける。
    そして，ちょっと気が向いたというわけである。


    錐は，平面上の図形 \( X \) の点全体と平面上にない１点 \( P \) が張る図形である。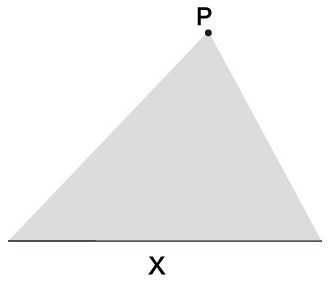
    このとき，\( X \) を「錐の底」，\( P \) を「錐の頂点」と呼ぶ。
    そして，底から頂点までの距離を，「錐の高さ」と呼ぶ。

    この錐の体積を求める方法は，
      「錐を底に平行にスライスして，
      　スライスした薄片の体積を足し合わせる」



    \( n \) 枚の等しい厚さの薄片にカットしたとする。
    各薄片に，頂点から底に向かって，つぎのように名づける：
      \( Y_1,\ Y_2,\ . . . ,\ Y_n \)
    また，各 \( Y_i \) につき， \( Y_i \) の \( X \) 側の断面を \( X_i \) とする。



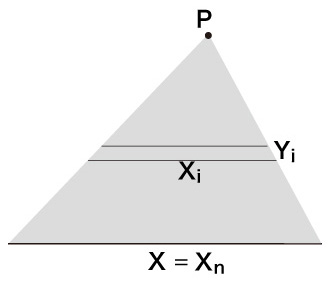    高さを \( h \) [単位長さ] とする。
    錐の底の面積を \( S \) [単位面積 = 単位長さ \( {}^2 \) ] とし，\( X_i \) の面積を \( S_i \) [単位面積] とする。

    \( X_i \) の \( X \) に対する相似比が \( i : n \) なので， \[ S_i = S \times \frac{ i^2 }{ n^2} \]
    スライスの数 \( n \) を大きくすると，\( Y_i \) は「柱」と見なせる。
    その体積 \( V_i \) [単位体積 = 単位長さ \( {}^3 \) ] は， \[ V_i = S_i \times \frac{ h }{ n } = \bigl( S \times \frac{ i^2 }{ n^2} \bigr) \times \frac{ h }{ n } \]
    よって，錐の体積 \( V \) [単位体積] は， \[ V = \lim_{n \to \infty}\ \sum_{i=1}^n V_i \\ = \lim_{n \to \infty}\ \sum_{i=1}^n \bigl( S\ h\ \frac{ i^2 }{ n^3} \bigr) \\ = \lim_{n \to \infty}\ \frac{ S\ h }{ n^3}\ \sum_{i=1}^n i^2 \\ = S\ h\ \lim_{n \to \infty}\ \frac{ 1 }{ n^3}\ \bigl( \frac{ 1 }{ 6 }\ n\ ( n + 1)\ ( 2n + 1) \bigr) \\ = S\ h\ \lim_{n \to \infty}\ \bigl( \frac{ 1 }{ 3 }\ + \frac{ 1 }{ 2\ n}\ + \frac{ 1 }{ 6\ n^2} \bigr) \\ = \frac{ 1 }{ 3 }\ S\ h \]