ここでは,<数は量の比>を立場とするときの「分数の割り算」の指導法を示す。
- 学習内容のアナウンス
本時は,「分数の割り算」を勉強します。
「割り算」のことばは,知っています。
分数は,これまでやってきました。
「分数の割り算」をそのまま書けば :「2/3÷5/4」
「2/3÷5/4」の (1) 意味と (2) 計算の仕方を勉強します。
- 「2/3÷5/4」の意味の学習
「÷」の使い方を確認しましょう。
「12×□=276」「□×12=276」の□を求める式を,「276÷12」と書きました。
これが「÷」の使い方です。
(要件:記号「÷」のこの意味が既習)
練習
- 5×□=35,□×5=35 → 35÷5
- 35÷5 → 5×□=35,□×5=35
「2/3÷5/4」の意味は,どうなるでしょう?
5/4×□=2/3,□×5/4=2/3 の□が 2/3÷5/4,ということになりますね。
練習
- 「2/3÷5/4」の計算のきまりを覚える
計算の仕方を自力で見つけるのは,実は難しいです。
(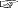 分数の求商公式の導き方) 分数の求商公式の導き方)
そこで,計算の仕方 (こたえ) を先に教えちゃいますね:
2/3÷5/4=2/3×4/5 (「ひっくり返して掛ける」)
言い回しを覚えましょう:
「分数の割り算は,割る方の分数をひっくり返して掛ける」
練習
- 「ひっくり返して掛ける」が確かにきまりになることの確認
- 5/4×□=2/3,□×5/4=2/3 の□が,2/3÷5/4。
2/3÷5/4 は 2/3×4/5 だと言いました。
2/3×4/5 を□に入れて,本当に等式が成り立つかな?
- □×5/4=2/3 の□に 2/3×4/5 を入れてみましょう。
2/3×4/5×5/4=2/3 の式になりました。
左辺に3つの分数が並んでいます。
この意味は何でしょう?
- 2×3×4の意味は何だったでしょう?
この意味は,「2倍して3倍して4倍」。
2倍して3倍して4倍は12倍だから,2×3×4=12。
(要件:記号「×」のこの意味が既習)
| 注意 : |
学校数学は,数の積を<倍の合成>として指導しないことになっている。
すなわち,「数は量の抽象」の立場から,数の積を「単位当たり量 × いくつ分」で教えている。
これだと,2×3×4 の解釈につぎのように窮することになるのだが,この不都合については目をつむるふうになっている。
| 2 |
× |
3 |
× |
4 |
| ↑ |
|
↑ |
|
↑ |
| 単位当たり量 |
|
いくつ分 |
|
? |
|
分数も同様です。
2/3×4/5×5/4 の意味は,「2/3倍して4/5倍して5/4倍」。
これは,言い換えると,「<3等分して2つ>をして,<5等分して4つ>をして,<4等分して5つ>をする」。
そして,2/3×4/5×5/4=2/3 ということは,これが<3等分して2つ>になるということ。
ほんとうにこうなっているかな?
図でやってみよう。
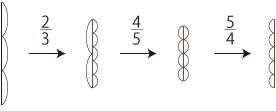
4/5×5/4 のところに注目しよう。
<5等分して4つ>をしてつぎに<4等分して5つ>をすると?
元に戻る。
つまり,変わらない。
(要件:「分数倍の逆倍」が既習)
2/3×4/5×5/4 から 4/5×5/4 が無くなるから, 2/3 が残る。
ということで,2/3×4/5×5/4 は,2/3。
- 5/4×□=2/3 の方は,どうだろうか?
5/4×□=2/3 の□に 2/3×4/5 を入れてみる。
ただし,今度は 2/3×4/5 のかわりに 4/5×2/3 を入れると,うまくいきます。
(要件 :「積の可換性」が既習)
5/4×4/5×2/3=2/3 の式になりました。
5/4×4/5×2/3 の意味は,<4等分して5つ>をして,<5等分して4つ>をして,<3等分して2つ>をする。
図でやってみよう。
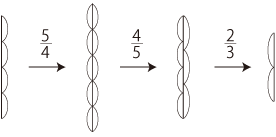
5/4×4/5 はどうなる?
<4等分して5つ>をして,つぎに<5等分して4つ>をすると?
変わらない。
5/4×4/5×2/3 から 5/4×4/5 が無くなるから, 2/3 が残る。
ということで,5/4×4/5×2/3 は,2/3。
- 練習
- 本時の学習内容の確認
- 5/4×□=2/3,□×5/4=2/3 の□が,2/3÷5/4。
- 「分数の割り算は,割る方の分数をひっくり返して掛ける」
|
現行の指導法は,<数は量の抽象>が立場である。
ただし,実際には<数は量の比>を都合よく混用している。
| |
「分数の割り算を,ここでは包含除で教えることにする」という言い回しに出会うことがあるが,「<数は量の比>を都合よく混用」の典型的な例がこれである。
|
数学は,<数は量の比>である。
本指導法は,この数学を直接指導するものなので,「一般的」で「シンプル」になる。
そのかわり「難しい」(?)。
現行の指導法は,数学を外しているので,「特殊な場面設定が必要」で「複雑」になる。
そのかわり「易しい」(?)。
さて,現行の指導法は「数学の教育的方便」として十分に割の合うものなのかどうか?
ここは読者自らが判断されたい。
|
 主題研究:分数の求商公式
主題研究:分数の求商公式
 主題研究:分数の求商公式
主題研究:分数の求商公式