Up 量の軸 作成: 2011-12-23
更新: 2012-02-15

    「数直線」は，自分を「＜量＞の軸」と読ませる。 体積の単位を添えたら＜体積＞の軸であり，重さの単位を添えたら＜重さ＞の軸である。

    しかし，現にあるものは，＜長さ＞のものさしである。 実際，描かれている目盛りを使って測れる量は，長さである。
    では，これが＜体積＞や＜重さ＞の軸であるとは，どういうことか？
    これの説明は，数学になる。
    以下，これを確認する。

    「＜重さ＞の軸」を例にする。
    「＜重さ＞の軸」として描くのは，つぎのものである：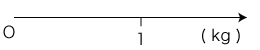


    この軸の上に，例えば「250ｇ」を目盛る場合，それはつぎの手順になる：
    1. Ｏの点から１の点までの距離を求める。
        ──これをｕとする。
    2. kg に対する 250ｇ の比を求める。
        ──これは 0.25。
    3. Ｏからの距離がｕの 0.25 倍になる点を，軸上に求める。
        ──この点に，「0.25」を目盛る。

    さて，これは数学として何をやっているのかというと，＜重さ＞と＜長さ＞の間の同型 (両者の量の構造に関する同型) を立てている。

    ＜重さ＞と＜長さ＞を，それぞれ ((Ｑ重さ, ＋ ), ×, (N, ＋, × ))，((Ｑ長さ, ＋ ), ×, (N, ＋, × )) とする。この例では，Nは小数である。

    ＜重さ＞と＜長さ＞の同型対応は，つぎの条件を満たす写像ｆ：Ｑ重さ → Ｑ長さ である：
    1. ｆは，Ｑ重さ と Ｑ長さ の間の１対１対応
    2. ｆ(ｘ＋ｙ）＝ｆ(ｘ) ＋ｆ(ｙ)　　（ｘ, ｙ ∈ Ｑ重さ)
    3. ｆ(ｘ × ｎ ）＝ｆ(ｘ) × ｎ　　（ｘ∈ Ｑ重さ，ｎ∈ N )

    ここで例にしている＜重さ＞の軸では，＜重さ＞と＜長さ＞の間の対応がつぎのようにつくられている：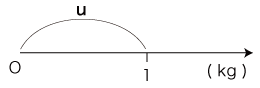
    1. kg に，任意の長さ ｕ を対応させる
    2. kg × ｎ に ｕ × ｎ を対応させる (ｎ∈ Ｎ)

    以上が，「量の軸を描く」の数学である。