Up 「比の３用法」の「数直線」図 作成: 2011-12-01
更新: 2012-02-21

    「２ｇの３倍は６ｇ」から，つぎの３タイプの問題が導かれる：
「２ｇの何倍が６ｇか？」
「２ｇの３倍は何ｇか？」
「何ｇの３倍が６ｇか？」
    ＜数は量の抽象＞の立場は，「比の３用法」の言い回しを以て，この３タイプの問題に対し「×」「÷」がつぎのように定まると説く：
「２ｇの何倍が６ｇか？」 比の第１用法：
何 ＝ ６ ÷ ２
「２ｇの３倍は何ｇか？」 比の第２用法：
何 ＝ ２ × ３
「何ｇの３倍が６ｇか？」 比の第３用法：
何 ＝ ６ ÷ ３
    さらに，この「比の３用法」を，つぎの「線図」に表す：


    そして，下辺の１と上辺の量の対応に対し，「１と見る/１あたり量」の読み方をする。


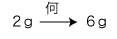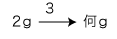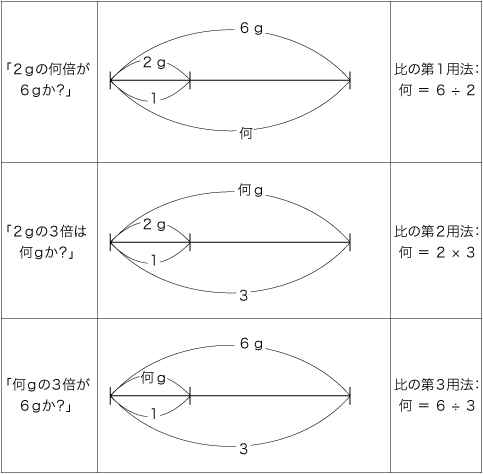
    「比の３用法」は，「形式不易の原理」と合わさって，分数・小数への適用となる：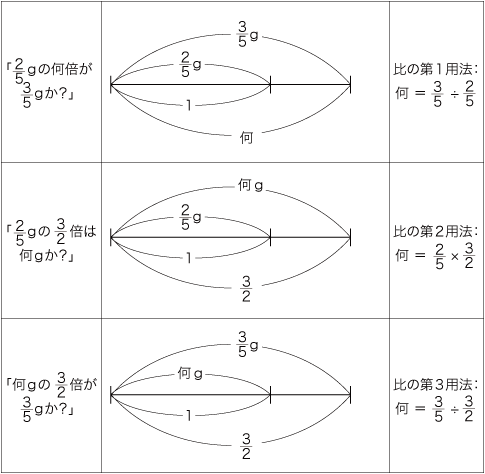



    上に示した「線図」は，今日「数直線」に替えられている：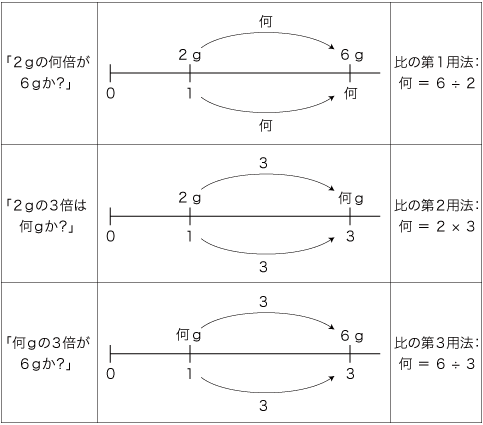





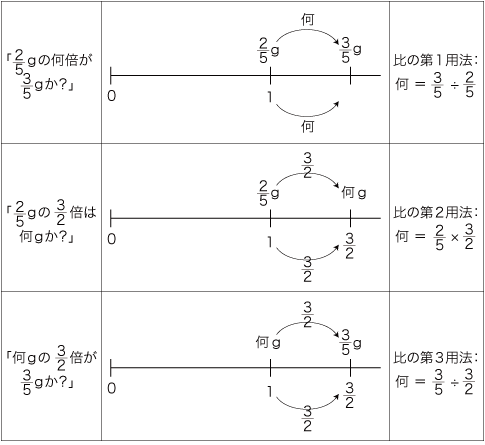
    「数直線」は，比例関係の図式に近づけたふうになっている。 すなわち，下辺と上辺の間の対応する倍が，書かれるようになる。
    しかしここで押さえるべきは，「数直線」は依然として「比の３用法」の表現であり，数学の明証に進んだわけではない，ということである。 「数直線」は「線図」と本質的に変わらない。

    ここは，再び学校数学の「×・÷」と数学の「×・÷」の違いを確認するところである。

    学校数学は，＜数は量の抽象＞を立場にする。 ＜数は量の抽象＞は，「比の３用法」(ないしこれの表現である「線図」「数直線」) を以て，「×・÷」を定める。 そしてこれは，数の積の意味を「１あたり量 × いくつ分」に定めるというものである。
    一方，数学は，＜数は量の比＞である。数の積の意味は，「倍の合成」である。
    ( 学校数学の「数」は，＜数は量の抽象＞)