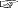文章題には,比例関係の問題が用いられる:
この問題に対し,「数直線」の図を,つぎの手順でつくる: 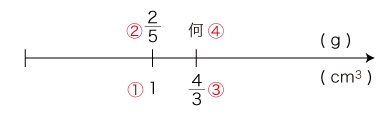
すなわち,問題を「1あたり 2/5gは,4/3 では何g?」のように読む。 そして,<量としての数>を下辺としたつぎの「数直線」を描く: 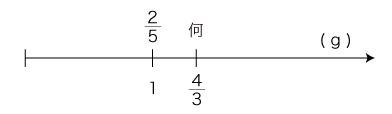
「数直線でかけ算」の立式指導は,この段階で「2/5 × 4/3」の立式に及ぶ。 あるいは,倍を書き入れたつぎの図を間に挿む場合もある: 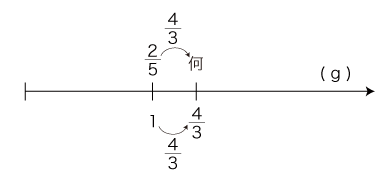
数学だと,ここはつぎの明証を経て数の積の立式に至るところである: 現行は,1 を明証できない。 内容が「比例関係」であり,そして「数直線」は「比例関係」を既習としないものになっているからである。 また,2 は明証無用になる。 数の「×」の意味を「1あたり量 ×いくつ分」にしているからである。 |