Up 「比の３用法」「形式不易の原理」：＜明証無用＞の装置 作成: 2011-12-01
更新: 2012-03-17

    ＜数は量の抽象＞は，量をリアルの側に措く写像理論である。
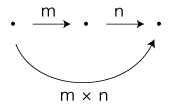
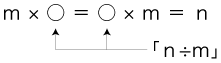    数は量の写像であり，数の算法は量の＜存在の事実＞の写像 ( ＜リアルの写し＞ ) である。
    分数・小数のかけ算・わり算」指導は文章題で始められるが，＜数は量の抽象＞の立場では，「かけ算・わり算」は＜リアルの写し＞として導入するのみだからである。

    この指導は，「比の３用法」「形式不易の原理」を暗黙に使うものになっている。 実際，以下に示すように，このときの「比の３用法」「形式不易の原理」は＜数は量の抽象＞の内容になる。

    「比の３用法」は，つぎの述定である：
    量の＜存在の事実＞に，「２ｇの３倍は６ｇ」がある。
    自然数の「×・÷」は，この事実の抽象をつぎの形に表すと決めたことで定まるところのものである：
    　　　３ ＝ ６ ÷ ２　（第１用法)
    　　　６ ＝ ２ × ３　（第２用法)
    　　　２ ＝ ６ ÷ ３　（第３用法)
    量の＜存在の事実＞に，「２/5ｇの 4/3倍は 8/15ｇ」がある。
    分数の「×・÷」は，この事実の抽象をつぎの形に現すと決めたことで定まるところのものである：
    　　　4/3 ＝ 8/15 ÷ ２/5　（第１用法)
    　　　8/15 ＝ ２/5 × 4/3　（第２用法)
    　　　2/5 ＝ 8/15 ÷ 4/3　 （第３用法)

    「比の３用法」には「形式不易の原理」が伴っている。 このときの「形式不易の原理」は，つぎの述定である：
    分数の「×・÷」の用法が自然数の「×・÷」の用法と同じになるのは，量がこのような存在だからである。

    この場合の「比の３用法」「形式不易の原理」は，これに対し「なに・なぜ？」を言うものではない。 ＜リアルの写し＞として，そのまま受け入れるものである。

    ＜リアルの写し＞は，これの適用領域が明証無用領域になるため，非明証性のもとになる。
    実際，＜数は量の抽象＞では，立式は形式感覚ないしノウハウで立てるものになる。


    数学では，「×・÷」の「形式不易の原理」は，つぎの内容になり，明証的である：
    数の各系 (自然数，分数，正負の数，複素数等) の「×・÷」は，つぎが成り立つようにつくられる：


    そして「比の３用法」は，記号「×・÷」の文法に他ならない。