一方,文章題を数の式に還元していく推理のプロセスは,指導内容とされていない。 特に,単位を外して数のみにする推理のプロセスは,指導内容とされていない。 《問題を見たら,それを裸にした数式を形式感覚で立てる》というふうになっている。 生徒は,「算数ができる」になるためには,この形式感覚を身につけねばならない。 <単位を外して数のみにする>は,数学としてなにをやっているのか? 生徒が自分の形式感覚にしていかねばならないこの数学は,どんな内容なのか? 量と<量としての数>の間に《単位に1を対応させる》同型を立て,この同型対応を以て,量の側の対象式・関係式を数の側に写す。──これが,その数学である。 すなわち,つぎのようになる:
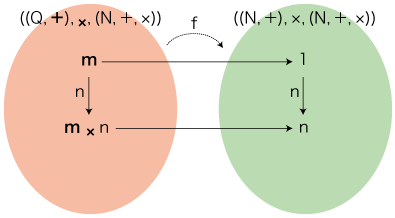
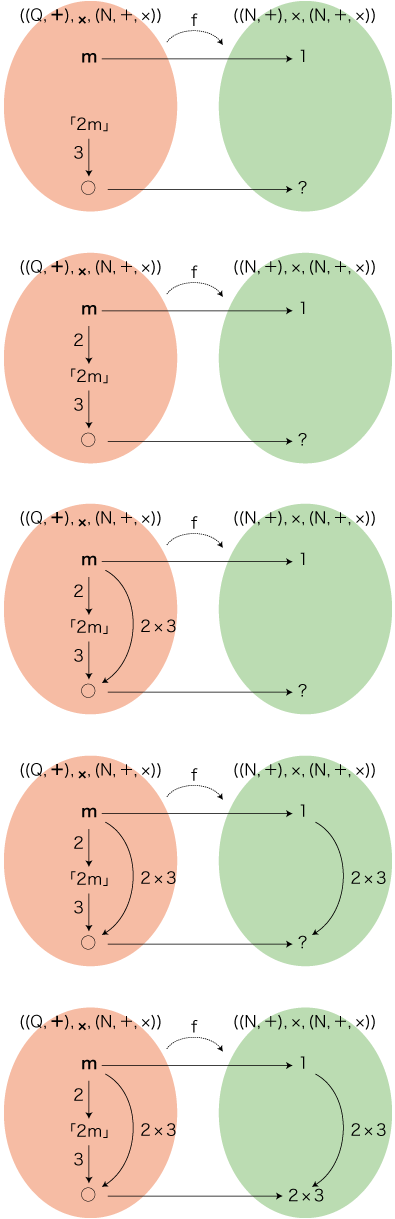
これに対し,数学の「量を数にする=単位を除く」は,どのようになっているか。 「2×3」の立式は,( (Q, +), ×, (N, +, ×) ) の側で済んでいる: 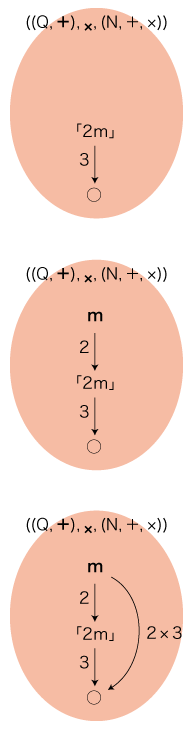
実際,量の系の中で倍関係を取り出したとき,それが数の積になっている。 「2×3」の立式において,( (N, +), ×, (N, +, ×) ) の導入は余計なことである。 《量の系の内部で数式を現す》──これが数の方法であり,要諦である。 実際,数がこのように用いられることが,数が<量の係数>として量の系の要素であることの意味なのである。 翻って,量の系の外に<量としての数>を措き,<量としての数>の中に数式を現すというのは,循環論法であり,無用・無駄のものである。 |