 「かけ算の順序」の数学とイデオロギーとモンスター ──「かけ算の順序」論争 解説) 「かけ算の順序」の数学とイデオロギーとモンスター ──「かけ算の順序」論争 解説)
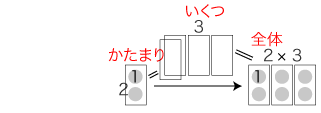
そしてこの論争での「かけ算に順序はある」の立場は,「かたまり × いくつ」「1あたり量 × いくつ分」の順序がかけ算の順序であると主張するものである。 以下,この主張が保てるものかどうかを見ていく。 (1) 「かたまり × いくつ」の場合 数の「×」の意味を「かたまり × いくつ」にする立場は,同時に「この順序がかけ算の順序である」と主張する立場である。 そして「かたまり × いくつ」の場合,「かけ算の順序」は確かにこの順序の他ではなくなる。 実際,「かたまり × いくつ」の図式では,「かたまり」の絵の前に「いくつ」の絵をおくことはできない。
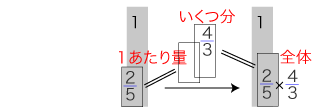
そしてこの順序は,数学の「かけ算の順序」と一致する。 しかし,この符合は,単に,数学の「かけ算の順序」を見て「かたまり × いくつ」を発案したためである。 実際,「かたまり × いくつ」は,自身の系の中で「かけ算の順序」を明証的にすることはできない。 存在論として自分を立てているからである。 (2) 「1あたり量 × いくつ分」の場合 「1あたり量 × いくつ分」は,つぎのような形を指す:
この立式を数学として行うと,つぎのようになる:
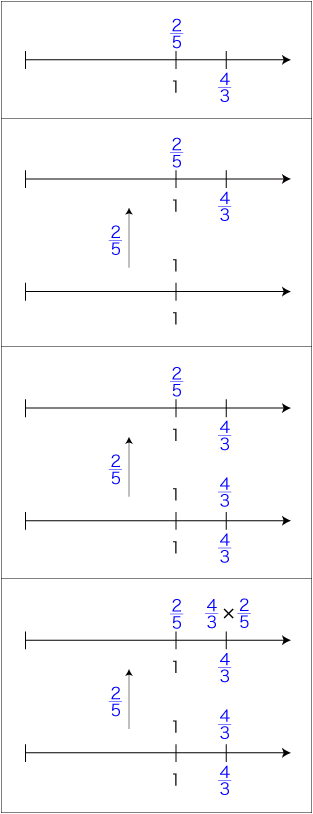
また,この手順を「数直線」に表すことにすると,つぎのようになる:
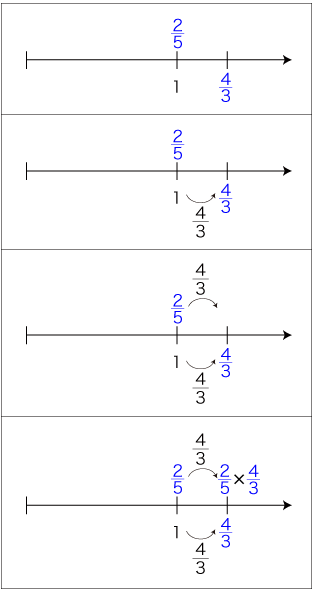
ここで,「1あたり量 × いくつ分」での 2/5 と 4/3 の順序が,数の積の式では逆になった。 「1あたり量 × いくつ分」の順序と積の式の2数の順序を同じにしたいならば,g/cm3 × 2/5 が比例関係であることを先に適用して,つぎの流れに替えることになる:
このように,「×」の意味を「1あたり量 × いくつ分」にするとき,数の積の式での2数の順序が定まらない。 特に,「1あたり量 × いくつ分」を立場にすることは,「かけ算に順序はない」を引き受けることである。 「1あたり量 × いくつ分」を立場とする者が「かけ算の順序」論争の場に進出するときは,「かけ算に順序はない」と言わねばならないのである。 |