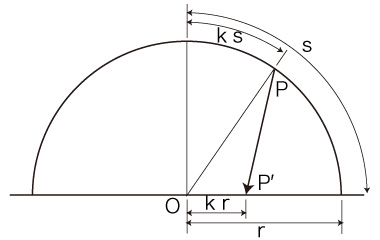
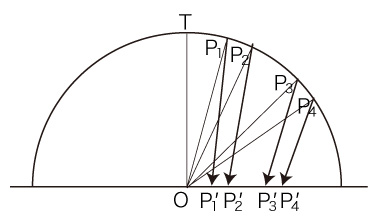
において,
\[
\newcommand{\overarc}[1]{\stackrel{\Large\mbox{$\frown$}}{#1}}
\overarc{P_1\ P_2} = \overarc{P_3\ P_4} \
\Longrightarrow\ \overline{P'_1\ P'_2} \ =\ \overline{P'_3\ P'_4} \
\]
となる。
証明:
\[
\newcommand{\overarc}[1]{\stackrel{\Large\mbox{$\frown$}}{#1}}
\overarc{T P_1} = k_1\ s ,\ \
\overarc{T P_2} = k_2\ s ,\ \
\overarc{T P_3} = k_3\ s ,\ \
\overarc{T P_4} = k_4\ s
\]
とすると,
\[
\newcommand{\overarc}[1]{\stackrel{\Large\mbox{$\frown$}}{#1}}
\overarc{P_1\ P_2} \
=\ \overarc{T P_2} - \overarc{T P_1} \
= k_2\ s - k_1\ s
= ( k_2 - k_1 )\ s
\]
同様に
\[
\newcommand{\overarc}[1]{\stackrel{\Large\mbox{$\frown$}}{#1}}
\overarc{P_3\ P_4}\ = ( k_4 - k_3 )\ s
\]
よって,
\[
k_2 - k_1 = k_4 - k_3
\]
そして,
\[
\overline{P'_1\ P'_2} \
=\ \overline{O P'_2} - \overline{O P'_1} \
= k_2\ r - k_1\ r \\
= ( k_2 - k_1 )\ r
= ( k_4 - k_3 )\ r \\
= k_4\ r - k_3\ r
=\ \overline{O P'_4} - \overline{O P'_3} \
=\ \overline{P'_3\ P'_4} \\
\]
|



